|
Learning objectives of this
article:
-
What is difference between nominal and effective
interest rate.
-
How effective interest rate is determined?
Contents:
Interest rates are typically stated as annual
percentages. The stated annual rate is usually
referred to as the nominal rate.
Interest may be compounded semiannually, quarterly,
and monthly, the interest earned during a year is
greater than if compounded annually. When
compounding is done more frequently than annually,
an effective annual interest rate can
be determined. This is the interest rate compounded
annually which is equivalent to a nominal rate
compounded more frequently than annually. The two
rates would be considered equivalent if both result
in the same compound amount.
Let r equal the effective annual interest rate, i
the nominal annual interest rate, and m the number
of compounding periods per year. The equivalence
between the two rates suggests that if a principle P
is invested for n years, the two compound amounts
would be the same, or
A small company has made a log-term investment of
$250,000. The interest rate is 12%, and interest is
compounded quarterly. Calculate annual
effective interest rate.
Solution:
|
In this example the investment is made
with a nominal interest rate of 12
percent per year compounded quarterly.
For this investment:
The effective annual interest rate is
calculated as follows:
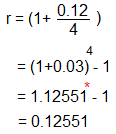
The effective annual
rate is 12.551 percent
*Future
value of $1 table - (1 + i)n
table, we can determine that (1+0.03)4
= 0.12551
|
|
|
|
Practice
Exercise: The nominal
interest rate on an investment is 7
percent per year. What is the effective
annual interest rate if interest is
compounded semiannually?
Answer: 7.122 percent |
|