|
Learning objectives of this
article:
-
What is an annuity?
-
How the future value of an
annuity is calculated?
-
Examples
Contents:
An annuity is a series of periodic payments.
Examples of annuities include regular deposits to a
saving account, monthly car, mortgage, or insurance
payments, and periodic payments to a person from a
retirement fund. Although an annuity may vary in
dollar amount, we will assume that an annuity
involves a series of equal payments. We will also
assume that the payments are all made at the end of
a compounding period. One may certainly argue
that end of one period coincides with the beginning
of the next period. The important point is that
payment does not qualify for interest in the
previous period but will earn full interest during
the next period.
Following is the illustration of a series of
payments R, each of which equals $1,000.
These might represent year-end deposits in a savings
account or quarterly tax payments by a self-employed
person.
Annuity
Future value of a lump sum investment is
explained on the
future value of a single sum page.
In this article future value or sum of an annuity is
determined.
The following formula is used to calculate future
value of an annuity:
|
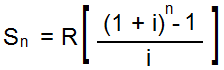
- R = Amount an annuity
- i = Interest rate per period
- n = Number of annuity payments
(also the number of compounding
periods)
- Sn = Sum (future
value) of the annuity after n
periods (payments)
|
Example:
A person plans to deposit $1,000 in a
tax-exempt savings plan at the end of this year
and an equal sum at the end of each following
year. If interest is expected to be earned at
the rate of 6 percent per year compounded
annually, to what sum will the investment grow
at the time of the fourth deposit?
Solution:
Example:
A teenager plans to deposit $50 in savings
account at the end of each quarter for the next
6 years. Interest is earned at a rate of 8
percent per year compounded quarterly. What
should her account balance be 6 years from now?
How much interest will she earn? Solution:
|
In this example:
- R = $50
- i = 0.08/4 = 0.02
- n = (6 years
×
4 quarters per year) = 24
S4 =
$50(30.42186*)
= $1,521.09
*
Future value of ordinary annuity
table Over 6-year period she will
make 24 deposits of $50 for a total
of $1,200. Interest for the period
will be $1,521.09 - $1,200.00 =
$321.09 |
The above formula can be solved for any of the
four parameters, given values for the other three.
For example, we might have a goal of accumulating a
particular sum of money by some future time. If the
rate of interest which can be earned is known, the
question becomes, what amount should be deposited
each period in order to reach the goal? In other
words formula can also be used to determine the size
of an annuity. For this purpose, formula can be
solved for R:
Suppose a corporation wants
to establish a sinking fund beginning at the
end of this year. Annual deposits will be
made at the end of this year and for the
following 9 years. If deposits earn interest
at the rate of 8 percent per year compounded
annually, how much money must be deposited
each year on order to have $12 million at
the time of the 10 deposit? How much
interest will be earned?
Solution:
- n = 10
- i = 0.08
- Sn = $12,000,000
- R = ?
The money to be deposited each year
(R) is calculates as follows:
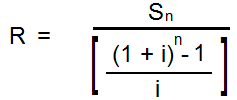
R = $12,000,000 / 14.48656*
R = 828354 *
Future value of ordinary annuity
table Since 10 deposits of
$828,354 will be made during this
period, total deposits will equal
$8,283,540. Because these deposits
plus accumulated interest will equal
$12 million, interest of $12,000,000
- $8,283,600 = $3,716,400 will be
earned. |
|